B. Rescue Niwen!
· 题意
给你一个字符串,求所有子字符串所构成的最长递增序列的长度。
INPUT : acbac
OUTPUT : 9 [ 'a', 'ac', 'acb', 'acba', 'acbac', 'c', 'cb', 'cba', 'cbac', 'b', 'ba', 'bac', 'a', 'ac', 'c'.]
解题思路
所有的子序列都是任一后缀序列的前缀,所以存在以下两个性质:
- 如果选择了
[L,R], 那么一定接着会选[L,R+1]、[L,R+2].... [L,n],原因是选择他们之后答案不会变的更劣。 - 如果选择到了
[L1,R1],如果你上一个串选择[L2,n],其中L2 < L1, 那么一定有[L1,R1]的字典序一定大于[L2,n]的字典序。设LCP(i,j)表示后缀[i,n]和[j,n]的最长公共前缀。所以应该有
s[l1 + LCP(l1,l2)] > s[l2 + LCP(l1,l2)]
我们可以从前往后计算,设 dp[i] 代表选择到第 i 个后缀序列最长上升子序列的长度。时间复杂度 O(n^2)
代码实现
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(s,val) memset(s, val, sizeof(s))
const int inf = INT_MAX;
const int MAXN = 5005;
int lcp[MAXN][MAXN], dp[MAXN];
int T, n;
string s;
//计算 [i,n] 和 [j,n] 两个子序列的大小关系
int larger(int i, int j){
return (lcp[i][j] != n - i and s[i + lcp[i][j]] > s[j + lcp[i][j]]);
}
int main(int argc, char * argv[]){
cin >> T;
while(T--){
cin >> n >> s;
for(int i = 0; i <= n; i++) for(int j = 0; j < n; j++) lcp[i][j] = 0;
//O(n^2)求lcp数组
for(int i = n-1; i >= 0; i--){
for(int j = n-1; j >= 0; j--){
if(i == j) lcp[i][j] = 1;
else if(s[i] == s[j]) lcp[i][j] = lcp[i+1][j+1] + 1;
}
}
int ans = n;
dp[0] = n;
for(int i = 1; i < n; i++){
dp[i] = n - i;
for(int j = 0; j < i; j++){
//转移方程: 枚举前面的后缀序列,计算后面包含这个子序列的答案
if(larger(i, j)) dp[i] = max(dp[i], dp[j]+ n-i - lcp[i][j]);
}
ans = max(ans, dp[i]);
}
cout << ans << endl;
}
return 0;
}
D. Mine Sweeper II
题意
给你一个扫雷地图A,B,每个 . 的权值为周围 8 个格子的含有地雷(X)的个数,如何在少于等于 [mn/2] 操作次数下让B图中的权值等于A的权值。
解题思路
重要的性质: 如果把所有的点变成叉,图的权值和不变,所以我们可以做以下考虑:如果可以在满足次数的条件下直接把 B 变成 A,那么可以直接转换。如果不可以,证明AB之间存在 x 个点的位置状态不一致,加入我们我们把求得 A 的反图, 那么此时B和A的反图之间所有相同的位置状态为 x, 不相同的位置为 mn/2 - x ,必定满足题意;
代码实现
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1004;
int T, m, n;
int valueA, valueB;
string A[MAXN], B[MAXN];
void printAns(bool needInv){
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(needInv) cout << (A[i][j] == '.' ? 'X' : '.');
else cout << A[i][j];
}
cout << endl;
}
}
int main(){
cin >> m >> n;
int diff = 0, maxOperation = m * n / 2;
for(int i = 0; i < m; i++) cin >> A[i];
for(int i = 0; i < m; i++) cin >> B[i];
for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) if(A[i][j] != B[i][j]) diff++;
if(diff <= maxOperation) printAns(false);
else printAns(true);
return 0;
}
F : Mr. Panda and Blocks
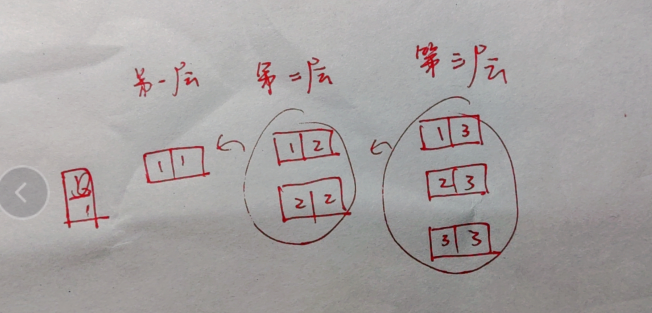
题意:
给你一个整数n,代表颜色种类数,然后定义长方体方块的左右两个子块的颜色是[1,1] [1,2] [1,3] [1,n] [2,3].…输出怎么放置使得每个颜色的所有子块都能形成一个城堡。(也就是相连块)
解题思路
构造题,可以使用以下方法来实现。对于每一个块, 让左右两端最大值来决定其放在第几层。
代码实现:
#include<iostream>
using namespace std;
int T, n, now = 1;
int main(){
cin >> T;
while(T--){
cin >> n;
cout << "Case #" + to_string(now++) + ":" << endl << "YES" << endl;
for(int j = 1; j <= n; j++)
for(int i = 1; i <= j; i++)
printf("%d %d %d %d %d %d %d %d\n", i,j ,i,1,j ,i,2,j);
}
}




