单源最短路径

单源最短路径

Tans 965 2022-03-21

背景知识

  1. 图简介：图由节点和边组成，边有方向的图称为有向图，边没有方向的图称为无向图，最短路径算法里可以把无向图视为双向连接的有向图。 边有权重的图称为有权图，边没有权重的图称为无权图，无权图可以视为边的权重均为1的图。
  2. 单源点最短路径：给定图中的一个节点，求该节点到其他所有节点的最短路径。

Dijkstra算法

Dijikstra算法就是为了解决单元最短路径问题。可以解决有向正权图和无向图，为什么不可以是负权图呢？我们后面再做讨论。
一.核心思想
我们设G=(V,E)为一个带权有向图，我们可以把图中的节点分为两组:

  • 一组为已经求出最短路径的顶点集合S，如果后续求出来一条最短路径那就把端点加入到集合S中，
  • 二组为未确定最短路径的节点集合U。
    同时，我们定义一个dist[i] 用来表示 从i节点到源点的最小距离。

二.步骤

  1. 初始化，源点加入到S中， 其他节点加入到U中。将起始节点start的所有可达节点的最短路径长度置为edge(start, arriveNode),
  2. 遍历curr可以达到的集合U中的节点(u)，更新过程中:
    如果dist[curr] + edge(curr,u) < dist[u],那么更新dist[u] = dist[curr] + edge(curr,u)
    最后找到U集合中距离源点路径最短的节点，即我们上面所求的dist[u]值最小节点u，加其入到S集合中，然后将 u 节点作为下次遍历的 curr 节点（也就是这个u节点是我们S集合中距离源点最长的节点了）
  3. 重复步骤2
    参考过程：
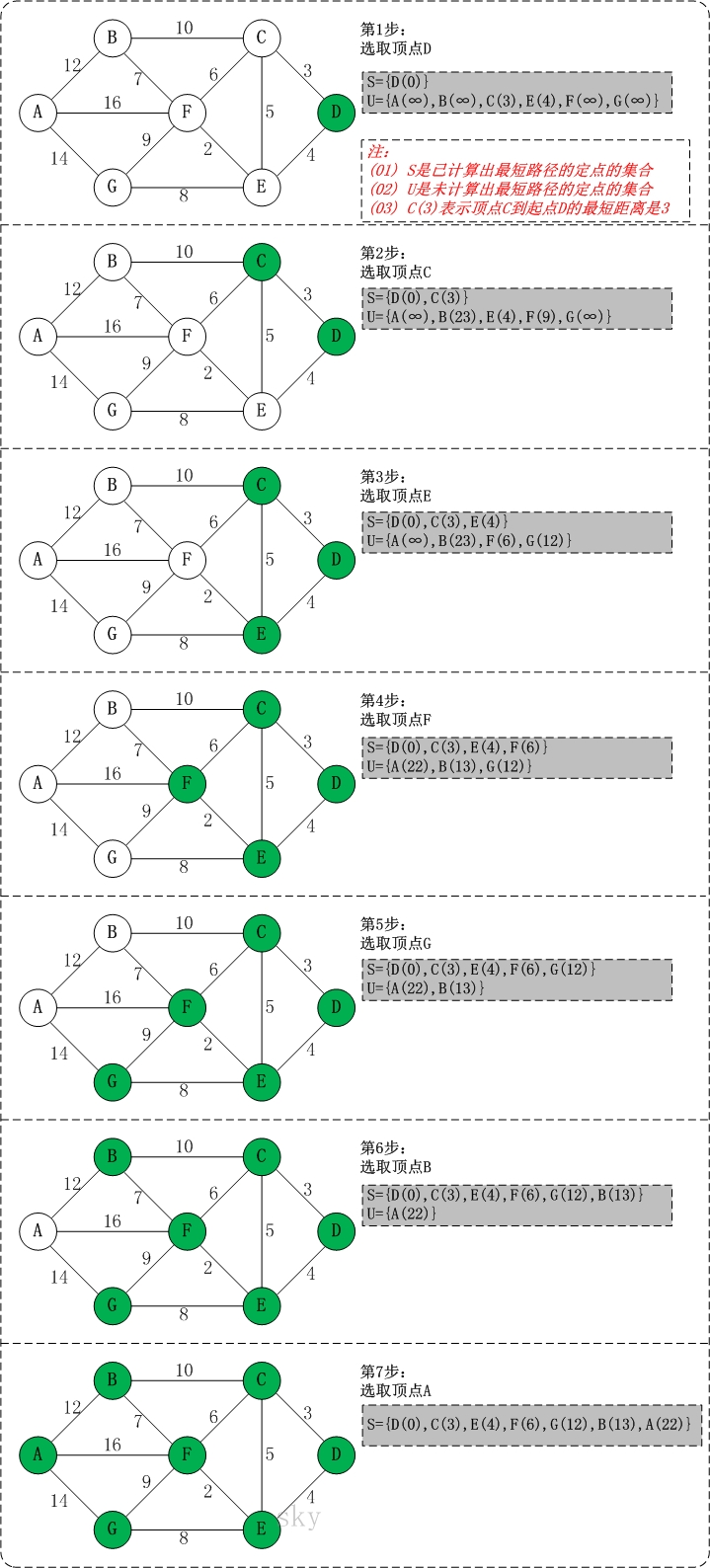
    image.png
    三.负权图无法判定的原因
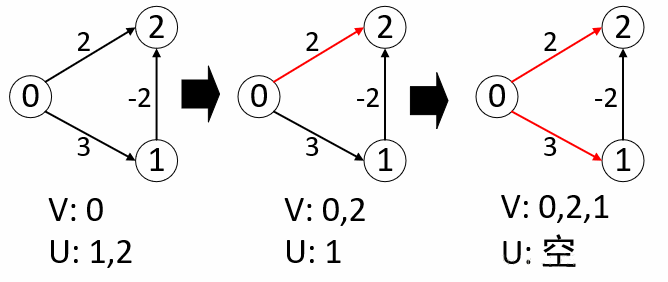
    image.png
    上图中，显然0-1-1是我们的最短路径，在此算法中第一步，我们按照步骤寻找U集合里面的最小路径，将节点0，2分别添加到S集合中，于是我们的curr节点变为2，然后我们把1节点加入，所以算法结束答案计算0-2的最短路径应该是2而不是1。综上，Dijkstra算法不适合于边权值为负值的图。
    四.有向图和无向图代码
    我们根据一个题目来理解用法：
    image.png
#include <iostream>
#include <climits>
using namespace std;
int n, m, start, endIndex;
int ways[2501][2501];			
long long dist[2501];
bool visited[2501] = {false};
int main(){
	cin >> n >> m >> start >> endIndex;
	//路径默认为极大值
	for (int i = 0; i <= 2500; i++)//init
		for (int j = 0; j <= 2500; j++)
			ways[i][j] = INT_MAX;
	fill(dist, dist + 2501, INT_MAX);
	//填充路径
	for(int i = 0; i < m; i++){
		int from , to, value;
		scanf("%d %d %d",&from, &to, &value);
		if(value < ways[from][to]){
			ways[from][to] = ways[to][from] = value; 
		}
	}
	//初始化
	dist[start] = 0;
	int min_value_index, min_value; //定义每次从集合U中最小路径下标以及最小路径
	while(true){
		min_value_index = -1;
		min_value = INT_MAX;
		//找到集合U中的最小路径下标和最小路径
		for(int i = 1; i <= n; i++){
			if(!visited[i] && min_value > dist[i]){
				min_value_index = i;
				min_value = dist[i];
			}
		}
		//如果所有节点都已经遍历过找到最小路径长度，那么直接跳出。
		if(min_value_index == -1) break;
		//将min_value_index元素加入到visited中
		visited[min_value_index] = true;
		//遍历更新U集合中每一个节点的距离
		for(int i = 1; i <= n; i++){
			if(!visited[i]){
				dist[i] = min(dist[i], dist[min_value_index] + ways[min_value_index][i]);
			}
		}
	}
	// print answer
	cout << dist[endIndex];
	return 0;
}

Bellman-Ford算法

Ford算法解决了Dijkstra算法的负权值不可计算的弊端。

算法 ACM C++