Trie树,即字典树、前缀树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较。
总的来说,Trie的思想是以空间换空间,利用字符串的公共前缀来降低查找操作带来的时间开销以达到提高效率的目的。
主要性质:
- 根节点不包含字符,除根节点之外每一个节点都只包含有且一个字符;
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串;
- 每个节点的所有子节点包含的字符都不相同;
一.字典树的定义
public class Trie{
Trie[] root; //孩子节点,代表下一个字符
boolean isPause; //是否终止
public Trie(){
root = new Trie[26];
isPause = false;
}
}
二.字典树的创建
void insert(String word) 向前缀树中插入字符串 word 。
栗子:好比假设有b,abc,abd,bcd,abcd,efg,hii 这6个单词,那我们创建trie树就得到:
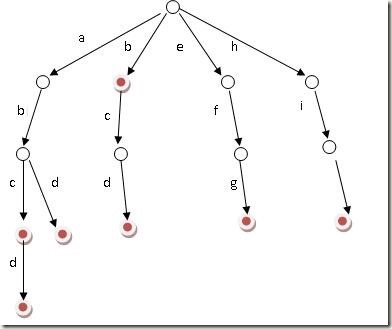
所以我们可以得到以下代码:
/** Inserts a word into the trie. */
public void insert(String word) {
int length = word.length();
Trie cur = this;
for(int i = 0; i < length; i++){
int index =word.charAt(i) - 'a'; //这里获得第i个字符的所在位置
if(cur.children[index] == null){//如果该分支不存在,那么创建
cur.children[index] = new Trie();
}
cur = cur.children[index]; //令cur指向当前单词,准备执行下一次操作
}
//单词插入完成后,需要将其此单词末尾字符的标记位 置true,代表此字符是单词的结尾
cur.isPause = true;
}
三.字符串的查找
/** Returns if the word is in the trie. */
public boolean search(String word) {
int length = word.length();
Trie cur = this;
for(int i = 0; i < length; i++){
int index = word.charAt(i) - 'a';
//如果下一个字符匹配不上,直接返回。
if(cur.children[index] == null){
return false;
}else{
cur = cur.children[index];
}
}
//遍历所有待查询单词的字符,返回待查询末尾字符是否为一个单词的结尾字符。
return cur.isPause;
}
四.字符串前缀的查找
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
int length = prefix.length();
Trie cur = this;
for(int i = 0; i < length; i++){
int index = prefix.charAt(i) - 'a';
//如果下一个字符匹配不上,直接返回。
if(cur.children[index] == null){
return false;
}else{
cur = cur.children[index];
}
}
//这里和字符串查询的区别在于, 只要满足一个单词的前缀就返回true
return true;
}
五.代码汇总
class Trie {
Trie[] children;
boolean isPause;
/** Initialize your data structure here. */
public Trie() {
children = new Trie[26];
isPause = false;
}
/** Inserts a word into the trie. */
public void insert(String word) {
int length = word.length();
Trie cur = this;
for(int i = 0; i < length; i++){
int index =word.charAt(i) - 'a';
if(cur.children[index] == null){
cur.children[index] = new Trie();
}
cur = cur.children[index];
}
cur.isPause = true;
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
int length = word.length();
Trie cur = this;
for(int i = 0; i < length; i++){
int index = word.charAt(i) - 'a';
if(cur.children[index] == null){
return false;
}else{
cur = cur.children[index];
}
}
return cur.isPause;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
int length = prefix.length();
Trie cur = this;
for(int i = 0; i < length; i++){
int index = prefix.charAt(i) - 'a';
if(cur.children[index] == null){
return false;
}else{
cur = cur.children[index];
}
}
return true;
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/
总结
时间复杂度:初始化为 O(1),其余操作为 O(|S|),其中 |S| 是每次插入或查询的字符串的长度。




